TURKISH JOURNAL OF ONCOLOGY

Summary

Kanserin erken tarama ve tanısına yardımcı ayırmalar kısaca “tanı testleri” olarak adlandırılmaktadır. Bu testlerin iç ve dış geçerlilikleri yüksek olmalıdır. Klinikte rutin kullanılan tanı testlerinin evrensel alt-üst sınır değerleri belirlenmiştir. Fakat pek çok yeni test için bu sınırları belirlemek gerekmektedir. Sınır değerleri parametrik ve non-parametrik istatistik yöntemlerle kolayca saptanabilir. Tıbbi testlerin performanslarının değerlendirilmesinde en önemli ve kullanışlı teknik “Receiver Operating Characteric” (ROC) eğrisi yöntemidir. ROC eğrisi tanı testlerinin güvenirliği ve genel doğruluğu (accuracy) açısından standart yöntem haline gelmiştir.

Summary

Introduction

“İstatistik” verileri derleme, sınıflandırma, tablo ve grafiklerle özetleme, olasılık yardımıyla tasarımlama ve gözlem ilkelerini saptama, örneklem bilgilerinin anlamlığını inceleme, yorumlama ve genelleme yöntemlerini veren bir bilimdir.[1] Kısacası istatistik, herhangi bir testin veya olayın nicel yönlerinin sayılarla anlatımıdır.

İstatistik yöntemleri diğer birçok bilimlerde olduğu gibi biyoloji, tıp, veterinerlik ve eczacılık bilimlerinde de yapılacak bilimsel araştırma ve değerlendirme çalışmalarında çok önemli yardımcı bir disiplindir. Tıpta ve eczacılıkta yeni bir tedavi yönteminin, yeni bir ilacın, yeni bir testin, ya da yeni bir ameliyat tekniğinin gerçek değeri ancak istatistik yöntemler yardımıyla en doğru biçimde belirlenebilir. İşte bu nedenlerle, tanınmış bir bilim adamının dediği gibi: “Günümüzde biyolojik ve tıbbi problemleri tarafsız ve eleştirici bir düşünce içinde sayısal esaslara göre değerlendirmeye alışmamış bir hekim, bir bilimin temsilcisi değil, ancak bir sanatın uygulayıcısı olabilir.”[2]

Biyoistatistik, “canlıların özelliklerinin ve bu özellikleri etkileyen diğer tüm öğelerin saptanması, sayılması, düzenlenmesi ve değerlendirilmesi ile nedensel bağlantıları çözümlemeye çalışan bilim dalı” olarak tanımlanabilir. Biyoistatistik iki ana biçimde kullanılmakta olup, bunlardan ilki verilerin toplanması ve dökümü, ikincisi ise çeşitli matematik yöntemlerle değerlendirilmesi şeklindedir.[3]

Dünya Sağlık Örgütü'nün tanımına göre tarama, uygulanması hızlı testlerle hastalık veya normal dışı özellikler taşıdığı o ana dek göze çarpmış olguların öncül belirlenmesidir.

Tarama ve tanı iki farklı kavramdır. Tarama ve tanıdaki ayırmalar kısaca “test” olarak adlandırılmaktadır. “Test”, yaptığı ayrım ve koyduğu tanı açısından güvenli olmalıdır. Başka bir deyişle testin iç ve dış geçerlilikleri yüksek olmalıdır.[4]

Tarama testleri, görünürde sağlıklı olan ancak belli bir hastalığı taşıması olası bireylerle, bu hastalığı taşımayan bireyleri ayırmaya olanak sağlamalıdır. Amaçları tanı koymak değildir. Taramada özellikle kesin sağlıklı olanların belirlenmesi önem taşımaktadır.

Tanıda, kuşkulu ve kesin hasta için ayrımlama aşaması gerekmektedir. Bu aşamada tanıyı kesinleştirecek, tedaviye alınacak hastaları ayrımlayacak yöntemlerden geçeceklerdir.[4]

Tanı testleri göreli olarak değerlendirilirler. Testin özellikleri ölçüt yöntemlerinin sonuçlarına dayalı hesaplamalarla elde edilir. Özellikler hasta/ sağlam ve test (+)/test (-) birlikte ele alınarak değerlendirilir. Tanı ve tarama testlerinin değerlendirilmesinde genellikle kullanılan ölçütler duyarlılık (sensitivity), özgüllük (specificity), genel doğruluk (accuracy), artı yorum gücü (positive predictive value) ve eksi yorum gücü (negative predictive value) kullanılır. Bu ölçütler için dört gözlü tablodan yararlanılarak testlerin sınır değerleri belirlenebilir (Tablo 1).

Tablo 1: Dört gözlü tablo

a) Duyarlılık (sensitivity) (%): Gerçek hastaları ayırabilme yeteneği
a / (a + c) = GP / (GP + YN)

b) Özgüllük (%) (specificity): Gerçek sağlamları ayırabilme yeteneği
d / (b + d) = GN / (GN + YP)

c) Artı yorum gücü (%) (+ predictive value): Test pozitifler içerisinde doğruluk oranı
a / (a + b) = GP / (GP + YP)

d) Eksi yorum gücü (%) (– predictive value): Test negatifler içerisinde doğruluk oranı
d / (c + d) = GN / (GN + YN)

e) Genel doğruluk (%) (accuracy): Testin toplam doğru tanı koyma oranı
(a + d) / (a + b + c +d) = (GP + GN) / (GP + GN + YP + YN)

Klinikte rutin kullanılan tanı testlerinin evrensel alt-üst sınır (normallik sınırları) değerleri belirlenmiştir. Bu sınırlar kullanılan kimyasal reaktiflerin özelliklerine ve testin yapıldığı ısı derecesine göre çok az farklılık gösterir. Bazı sınırlar dünyada standardize edilmiştir (örn.: glikoz, karaciğer enzimleri, hemoglobin miktarı vb.). Buna karşılık tanıda kullanılmak üzere pek çok yeni test kullanıma sunulmaktadır. Fakat bu testlerin henüz standardize alt-üst sınırları belirlenmemiştir. Bu nedenle testlere ait sınırları saptamak için her laboratuvarın kendi sınırlarını belirlemesi gerekmektedir.

Bir testin alt-üst sınırlarının belirlenmesi için sağlıklı toplumdan rastgele seçilmiş deneklerin sayısı ana yığını temsil edecek büyüklükte olmalıdır.[5] Elde edilen test sonuçlarının tanımlayıcı istatistikleri (aritmetik ortalaması, standart sapması, ortanca değeri, persantileri ile en düşük ve en yüksek değeri) hesaplanır.[6] Hasta seçimi belirlendikten sonra dağılım sınanarak normal dağılıma uymayan gruplarda normal dağılımı elde edebilmek için istatistiksel yöntemlerle dönüşüm yapılmalıdır.[7] Laboratuvar test sonuçlarının ışığında aşağıdaki diyagrama göre alt-üst sınır değer belirleme yöntemlerinden biri seçilir (Şekil 1).

Sekil 1: Kesim (tahmini referans) değerlerinin belirlenmesinde izlenecek yol.

Sınır Değerlerin Saptanma Yöntemleri
Sınır değerlerin saptanma yöntemleri, “Macrophage Migration Inhibitory Factor” (MIF) tümör marker değişkeninin (sürekli değişken) kolon kanseri tanısında kullanımına ilişkin bir örnek verilerek açıklanacaktır.

Kolon kanseri tanısı konmuş 35 hasta ve 20 sağlıklı kişide (kolon kanseri olmayan) MIF değerlerinin ölçüldüğünü ve elde edilen değerlerin aşağıdaki tablolarda (Tablo 2, 3) özetlendiği varsayalım.

Tablo 2: Hasta grubu (Kolon kanseri hastaları)

Tablo 3: Kontrol grubu (Kolon kanseri olmayan)

Bu örnek üzerinden üç ayrı yöntem irdelenecektir.

Yöntem 1. (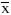 1,96* sd)
MIF değişkeninin kontrol ve hasta gruplarında normal dağılıma uygun olup olmadığı “Kolmogorov-Smirnov tek örneklem” testi ile sınanır. Sınama sonucunda kontrol ve hasta grubunun normal dağılıma uygunluk gösterdiği belirlenirse kontrol grubunda teste ait “aritmetik ortalama + (1,96) x standart sapma” ifadesi yardımıyla testin üst sınırı belirlenir. Hasta MIF verileri ile “aritmetik ortalama - (1,96) x standart sapma” ifadesi kullanılarak testin alt sınırı saptanır (Şekil 2).

Sekil 2: Hasta ve kontrol test değerlerinin kuramsal dağılımı.

Örneğimizde, MIF değişkeni “ Kolmogorov-Smirnov tek örneklem” testi sonucunda kontrol grubunun normal dağılıma uygunluk göstermektedir (p=0,983). Fakat hasta grubunun normal dağılıma (p=0,007) uygunluk göstermediği görülmektedir. Bu nedenle, logaritmik dönüşüm yapılması gerekir. MIF değişkeni logaritması hesaplanarak “logMIF” değişkenine dönüştürüldü.

Logaritmik dönüşüm yapıldığında hem kontrol grubunun (p=1,0), hem de hasta grubunun (p=0,222) “logMIF” değişkeninin normal dağıldığı gözlenir. Daha sonra kontrol grubunun “log-MIF” değişkenine ait “aritmetik ortalama + (1,96) x standart sapma” ve hasta grubuna ait “aritmetik ait “aritmetik ortalama -(1,96) x standart sapma” ifadeleriyle tahmini kesim (tahmini referans) değerlerinin bulunduğu aralık belirlenir. Bu sınırlar civarındaki test değerlerine ait duyarlılık ve özgüllükler hesaplanır. Duyarlılık ve özgüllüğü aynı anda yüksek olan test değeri, kesim (tahmini referans) değer olarak belirlenir.

MIF değerleri
Kontrol: Aritmetik ortalama (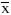 ): 12,43 ng/mL
Standart sapma (sd): 3,20
Hasta: Aritmetik ortalama (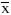 ): 25,21 ng/mL
Standart sapma (sd): 22,08
Üst sınır: 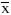+ (1,96*SD) = 12,43 + (1,96*3,20) = 18,7 ng/mL (Kontrol grubundan)
Alt sınır: 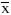- (1,96*SD) = 25,21 - (1,96*22,08) = 0 ng/mL (Hasta grubundan)
Örnekte grupların birinde normal dağılım olmadığı için,

LogMIF değerleri
Üst sınır: 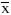+ (1,96*SD) = 1,0814 + (1,96*0,1074) = 1,2919 ng/mL; 10 tabanına göre antilog değişimi = 19,58 bulunur. (Kontrol grubundan)

Alt sınır: 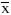- (1,96*SD) = 1,2906 -(1,96*0,2899) = 0,7224 ng/mL; 10 tabanına göre antilog değişimi = 5,28 bulunur. (Hasta grubundan)

Bulunan bu kesim (tahmini referans) değerleri olan 5,28 (≈5) ile 19,58 (≈20) arasında 4 kesim (tahmini referans) noktası için duyarlılık ve özgüllükler hesaplanır. Kesim (tahmini referans) noktaları aşağıdaki gibidir (Tablo 4).

Tablo 4: Tahmini kesim noktalarının duyarlılık ve özgüllükleri

Tablodan görüldüğü gibi tanı değerlerinin her ikisini en yüksek yapan sınır değer 10 -15 aralığında olduğu görülmektedir. Bu aralığı daha ayrıntılı incelersek Tablo 5'deki sonuçları elde ederiz.

Tablo 5: Tahmini kesim noktalarının duyarlılık ve özgüllükleri

En iyi kesim değerinin ≈14 ng/mL olduğu görülmektedir.

Yöntem 2.
Sınır değerlerin belirlenmesinde testin hasta ve kontrol sonuçlarının ortanca (50. persantil) değeri baz alınarak 2,5. -97,5. persantil değerleri, persantil tablosu kullanılarak hesaplanır.[9] 2,5 ve 97,5. persantil değerleri temsil edebilecek gözlem sayısı yoksa 5. -95. veya 25. -75. persantil değerleri gibi alt-üst sınırlar kullanılabilir. Kontrol grubunun maksimum değerine yakın değerler içinden belirlenen kesim değeri üst sınır; hasta grubunun minimum değerine yakın değerler arasından alt sınır belirlenir.[10] Örnekte her ne kadar dönüşüm sonrası normallik koşulu gerçekleşmiş olsa da, yöntem iki aynı örnek üzerinden açıklanacaktır.

Örnekteki kontrol grubunun MIF değerlerine göre:

90. persantil: 16,33 ng/mL
95. persantil: 20,96 ng/mL
97,5. persantil: 21,20 ng/mL
Örnekteki hasta grubunun MIF değerlerine göre:

2,5. persantil: 8,0 ng / mL
5. persantil: 8,8 ng/mL
10. persantil: 10,0 ng/mL

Bulunan bu kesim değerleri olan 8,0 ile 21,20 (≈22) arasında 4 kesim (tahmini referans) noktası için duyarlılık ve özgüllükler hesaplanır. Tahmini kesim noktaları Tablo 6'daki gibidir. Tabloda görüldüğü gibi en uygun kesim değerinin ≈13 ng/mL olduğu görülmektedir.

Tablo 6: Tahmini kesim noktalarının duyarlılık ve özgüllükleri

Yöntem 3.
ROC (Receiver Operating Characteristics) eğrisinin çözümleme yönteminde, belirli bir tanım aralığında sürekli değerler alan bir değişkenin (sürekli değişken) tanı testi olarak kullanımı amaçlanmaktadır.[11] Receiver Operating Characteristic (ROC) eğrisinden yararlanılarak sınır değerlerinin belirlenmesinde istatistik paket program veya grafik çizerek hesaplama yöntemi kullanılır. Bu eğrinin çizimi için kesim (tahmini referans) noktalarına ihtiyaç vardır.

ROC çözümleme yöntemini, yukarıdaki örnekle açıklayalım.

Örneğimizdeki hasta ve kontrol grubuna ait MIF değerlerini küçükten büyüğe sıraya dizilerek sıralı değerlerden oluşan tablolar elde edilir (Tablo 7, 8).

Tablo 7: Hasta grubu sıralı değerler

Tablo 8: Kontrol grubu sıralı değerler

Hasta ve kontrol gruplarına ait tanımlayıcı istatistikler aşağıdaki gibi elde edilir.

Çeşitli pozitiflik sınır değeri için (cut- off values, kesim değerleri) duyarlılık ve (1 – özgüllük) değerleri hesaplanır.

Hasta ve kontrol grupları birlikte ele alındığında, en küçük değer 8,0 en büyük değer ise 95,0 olarak belirlenir, 8,0 ile 95,0 arasında en az 10 pozitiflik sınır değer tesbit edilir. Örnek için 8, 10, 12, 14, 16, 18, 20, 25, 30 ve 40 pozitiflik sınır değerleri kullanılmaktadır. Kesim (tahmini referans) değerlerinin sayısının artması ROC eğrisinin duyarlılığını arttırmaktadır.

Pozitiflik sınır değeri (cut-off value) 16 için duyarlılık ve özgüllük değerlerini hesaplamak için: MIF ≥ 16 ise test sonucu pozitif (kişi hasta) aksine MIF ≤ 16 ise test sonucu negatif (kişi sağlıklı) kabul edilecektir. Hasta grubunda 19 kişide, kontrol grubunda ise 2 kişide MIF ≥16'dır.

16 sınır değeri için; doğru pozitif, yanlış pozitif, yanlış negatif ve doğru negatif sayıları tabloda özetlenmiştir (Tablo 9).

Tablo 9: Örneğe ait dört gözlü tablo

Duyarlılık = 19 / 35 = 0,54

Özgüllük = 18 / 20 = 0,90

(1 – özgüllük ) = 1 – 0,90 = 0,10

16 sınır değeri için (0,10; 0,54) noktası elde edilir.

ROC eğrisinin çizileceği noktalar, diğer tüm sınır değerleri için benzer işlemleri tekrarlayarak belirlenir.

Duyarlılık (y) ekseninde, (1 – özgüllük) değerleri ise (x) ekseninde temsil edilir.

Tüm sınır değerleri için elde edilen duyarlılık, özgüllük ve (1 – özgüllük) değerleri Tablo 10'da verilmektedir.

Tablo 10: Sınır değerleri için elde edilen duyarlılık, özgüllük ve (1 – özgüllük) değerleri

10 ayrı pozitiflik sınır değeri için elde edilen duyarlılık ve (1 – özgüllük) koordinat değerlerini kullanarak ROC eğrisi çizilir (Şekil 3).

Sekil 3: MIF tanı testine ait ROC eğrisi.

MIF tümör marker değişkeninin tanı değerinin gücü (hasta ve sağlamı ayırt edebilme gücü) ROC eğrisinin altında kalan alan ile ifade edilir. Alan değeri 1'e yaklaştıkça tanı değeri yükselir. %100'lük tanı gücünde alan değeri 1'e eşit olur.

Yukaridaki tablodan görüldüğü gibi en uygun kesim değeri ≈14 ng/mL olduğu görülmektedir.

Introduction